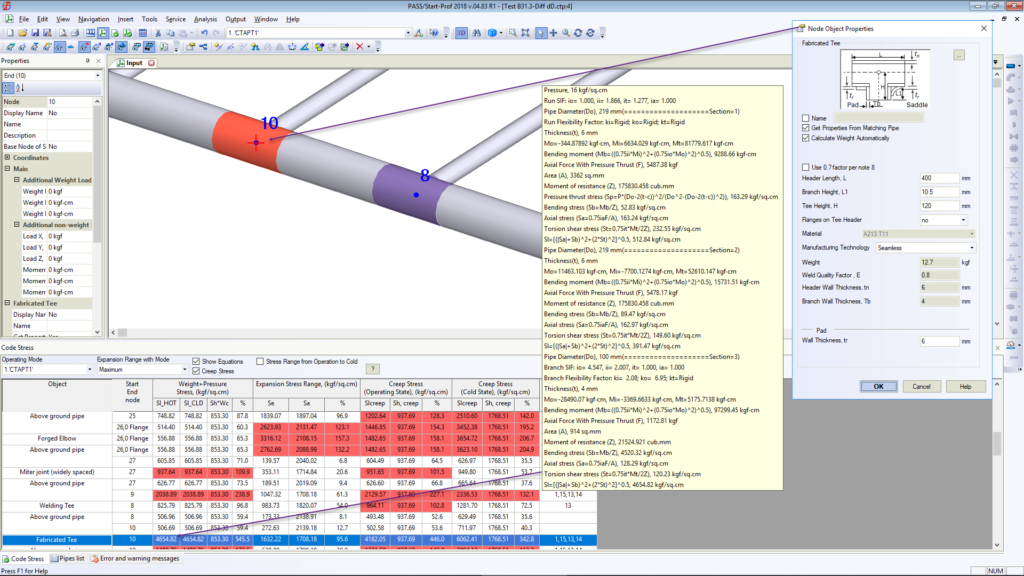
Several ASME B31 & EN 13480 Issues Needed to Know for Pipe Stress Engineer
Effective Tee Branch Section Modulus Issue in ASME B31.3-2016
This issue led to serious under-estimation of sustained and occasional bending stresses at reducing intersections.
ASME B31.1-2018 code requires to calculate the bending stress from thermal expansion for reducing tee branch by equation (all symbols are taken as per ASME B31.3-2016 code for better understanding):
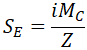
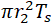
Z is section modulus, where effective branch wall thickness is

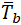
is the thickness of pipe matching branch,

is the thickness of the pipe matching run of tee or header.
What is the effective branch wall thickness? The answer is given in L.C. Peng “Pipe Stress Engineering” book, 4.5.1. The idea is the following. Bending stresses must be checked in two potential locations of failure:
- In branch and header pipes junction, zone 1
- in branch pipe next to the junction, zone 2
The failure will happen in zone 1 if the stress intensification factor is high. But if the stress intensification factor is not significant, the failure will happen in zone 2. The code should check the bending stress in both locations.
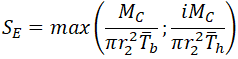
ASME B31.1-2018 use simplified equation 104.8.3, 104.8.4C:

Where effective branch wall thickness is

For sustained stress equations for 1 and 2 zones should be:

The simplified equation in ASME B31.1-2018 104.8.1, 104.8.4
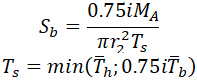
Now let’s check ASME B31.3-2016 code. As it uses two stress intensification factors (in-plane and out-plane), the equation for bending stress in locations 1 and 2 should be:
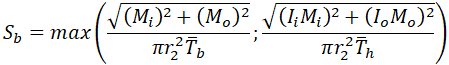
But ASME B31.3-2016 code offers for reducing tee bending stress from sustained loads the equation 23b2

Sustained in-plane and out-plane SIFs:
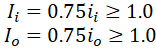
Effective section modulus of branch

Effective wall thickness is determined according to 319.4.4 (c)
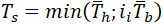
If we convert these equations back to the stresses in 1 and 2 locations, we will have
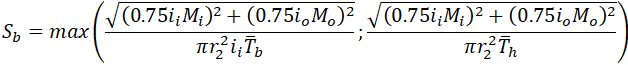
For location 2 stresses become incorrect:
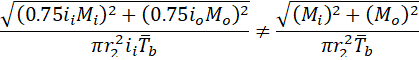
Let’s assume that Mo=0, in this case, we get underestimated by 25% bending stress in the branch pipe
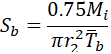
Instead of correct stress value
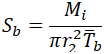
If we take Mi=0, we get bending stress in the branch pipe
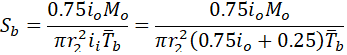
If we assume that io=1.4, then we get bending stress underestimated by 19%

To partially fix this problem we should change the equation 23b2 for effective wall thickness in 320.2 to
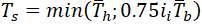
But in this case, the out-of-plane bending stress in branch connection will be overestimated. If we assume that io=3.0 the out-of-plane bending stress in branch pipe will be overestimated 25%:
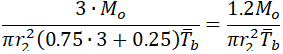
To fix this problem we should correct the bending stress equation in 320.2 to
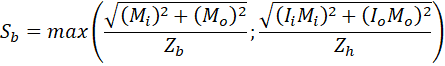
Zh – Header section modulus, Zb – Branch section modulus.
Unfortunately, these corrections can’t be made in the software. The ASME B31.3 code revision needed.
Fortunately, a new code ASME B31J-2017 has been released. Using this code we can bypass this problem. We recommend activating the “ASME B31J” option in PASS/Start-Prof software.
If this option is activated, the accurate section modulus will be used for header and branch pipes:

Also if “ASME B31J” option is activated then all tees are automatically modeled with simultaneous use of run and branch springs with flexibilities and stress intensification factors calculated according to ASME B31J code requirement:

Start-Prof software allows activating the “ASME B31J” option for all ASME B31 codes and EN 13480! If some of k-factor becomes less than 1.0 Start-Prof assumes this spring as rigid: